regola carattere

statistica descittiva

medie di posizione

moda
mediana

sommatoria e produttoria

sommatoria
produttoria

medie algebriche

media aritmetica
media quadratica
media geometrica
media armonica
proprietà delle medie
ordine delle medie
media generalizzata

medie

In statistica, si chiamano medie quei valori che offrono una sintesi di un insieme di dati.

Queste vengono dette anche indici di posizione, o indicatori di posizione, o indici di tendenza centrale o misure di tendenza centrale.

Si distinguono due tipi di medie:

medie di posizione: che considerano solo certi valori e, in generale, non si ottengono manipolando matematicamente i dati.
medie algebriche: che considerano tutti i valori e si ricavano applicando formule matematiche.

Qualunque sia la media, essa è sempre espressa nella medesima unità di misura delle modalità da cui si è ricavata.

tipi di media

medie di posizione

Le medie di posizione considerano soltanto alcuni dati e non si occupano di manipolarli con operazioni matematiche bensì soltanto della loro posizione o ripetizione nella distribuzione.

moda

La moda (detta anche norma) è la modalità che si presenta il maggior numero di volte.

Il suo significato in statistica è simile a quello in gergo comune. Si desume dalla sua definizione che la moda è la modalità cui è associata la frequenza maggiore.

Nel caso sia una la modalità che presenta la frequenza maggiore di tutte le altre, allora la distribuzione si dirà unimodale, se due bimodale, se tre trimodale, ecc. ecc.

Continuiamo con l'esempio dell'indagine che ha osservato il numero di animali domestici intervistando 10 rappresentanti di classe di un istituto susperiore. Aveva prodotto la seguente distribuzione di frequenze:

x	f
1	2
2	5
3	3

Come si osserva, la modalità che ricorre più spesso è 2 animali domestici ovvero 5 volte, quindi:

moda = 2animali

La moda è l'unica tra le medie che ammetta caratteri sia quantitativi, sia qualitativi.

mediana

La mediana è la modalità che si trova al centro di una distribuzione ordinata.

Per la mediana (e soltanto per questa media) è indispensabile che le modalità siano in ordine (crescente o decrescente), essa è quella che si trova al centro. Ne deriva che il carattere bisogna che sia quantitativo o qualitativo ordinabile.

Di fatto, la mediana divide la distribuzione in due, essa lascia prima di sé la metà delle modalità e dopo di sé l'altra metà.

In altre parole, è quella modalità la cui frequenza percentuale cumulata vale 50%.

Essendo la mediana la modalità centrale, bisognerà distinguere i casi di un numero totale di modalità dispari o pari.

Se questo è dispari, allora esiste una modalità centrale che ne lascerà tante prima quante dopo
Se pari, avremo non una, ma una coppia di modalità che dividono in due la distribuzione.

n dispari

Quando n è dispari, la mediana, è la modalità nella posizione $\frac{n + 1}{2}$

1ª	2ª	3ª	4ª	5ª	6ª	7ª

x₁	x₂	x₃	x₄	x₅	x₆	x₇

Nel caso siano in tutto 7 modalità, la mediana è la 4ª modalità (ne conta 3 prima e 3 dopo):

$M e = x_{\frac{n + 1}{2}} = x_{\frac{7 + 1}{2}} = x_{\frac{8}{2}} = x_{4}$

Portiamo ad ulteriore esempio una indagine avente come carattere il numero di pizze consumate nell'ultimo mese. Ha prodotto la seguente distribuzione unitaria:

x
5
1
4
2
4
5
2
4
3
1
4

che una volta ordinata appare così:

x_i	x
x₁	1
x₂	1
x₃	2
x₄	2
x₅	2
x₆	3
x₇	4
x₈	4
x₉	4
x₁₀	5
x₁₁	5

Essendo n = 11 (dispari), allora la mediana è quella modalità che si trova nella posizione $\frac{11 + 1}{2}$ (lascia 5 modalità prima e 5 dopo):

$M e = x_{\frac{11 + 1}{2}} = x_{\frac{12}{2}} = x_{6} = 3 pizze$

Avendo una distribuzione di frequenze, per trovare la modalità che occupa la posizione centrale, ci si avvale delle frequenze cumulate, controllando la modalità a cui corrisponde la frequenza cumulata che raggiunge la posizione cercata:

Per trovare la 6ª modalità, si cumulano le frequenze sino a raggiungere 6, la mediana è la modalità corrispondente (3 pizze):

x	f	f_c
1	2	2
2	3	5
3	1	6
4	3
5	2
∑	11

n pari

Quando n è pari, le modalità centrali sono due, cioè quelle nelle posizioni:

$\frac{n}{2}$
$\frac{n}{2} + 1$

Di regola, la mediana è stimata in funzione di questi due valori centrali perchè sia un valore compreso tra i due e convensionalemente si opera la loro semisomma (o media aritmetica che dir si voglia).

1ª	2ª	3ª	4ª	5ª	6ª	7ª	8ª

x₁	x₂	x₃	x₄	x₅	x₆	x₇	x₇

Nel caso siano in tutto 8 modalità, le centrali sono la 4ª e la 5ª (ne contano 3 prima e 3 dopo) e la mediana:

$M e = \frac{x_{\frac{n}{2}} + x_{\frac{n}{2} + 1}}{2} = \frac{x_{\frac{8}{2}} + x_{\frac{8}{2} + 1}}{2} = \frac{x_{4} + x_{5}}{2}$

Portiamo lo stesso esempio dell'indagine sul numero di pizze consumate nell'ultimo mese, svolto su un secondo gruppo di persone. Dalle interviste di è desunta la sequente distribuzione di frequenze:

x	f	f_c
1	2	2
2	3	5
3	4	9
4	6	15
5	3
∑	18

Essendo n pari (18), le modalità centrali sono 2:

$x_{\frac{18}{2}} = x_{9}$
$x_{\frac{18}{2} + 1} = x_{10}$

Usando le frequenze cumulate si vede che la 9ª modalità è l'ultimo dei 3, e la successina, la 10ª è il primo dei 4. Infatti:

$M e = \frac{x_{\frac{18}{2}} + x_{\frac{18}{2} + 1}}{2} = \frac{x_{9} + x_{10}}{2} = \frac{3 + 4}{2} = 3.5 pizze$

proprietà della mediana

La mediana è quel valore centrale il quale, considerando gli scarti assoluti tra ciascun dato ed essa rende minima la loro somma.

Disponendo cioè di un insieme di valori e volendo che la somma delle loro distanze (scarti, differenze, deviazioni) assolute da un medesimo valore centrale sia la più piccola possibile, ebbene tale valore è la mediana.

esempio d'uso della mediana

Un distributore dovrà fornire 6 attività commerciali tutte lungo un'unica strada, partendo dalla prima, misura le loro distanze progressive (in km) ottenendo:

attività	progressiva
1	0
2	9
3	15
4	17
5	33
6	40

Vorrebbe costruire un magazzino in maniera che sia più vicino possibile alle 6 attività, quindi tale che la somma delle distanze assolute delle attività dal magazzino sia la minima.

Si cerca allora la mediana:

$M e = \frac{x_{\frac{6}{2}} + x_{\frac{6}{2} + 1}}{2} = \frac{x_{3} + x_{4}}{2} = \frac{15 + 17}{2} = 16 k m$

Costruendo il magazzino alla kilometrica 16 (a 16 km dalla prima attività) si ottiene che:

x_i	x	scarto assoluto dalla mediana
x₁	0	\|0-16\| = 16
x₂	9	\|9-16\| = 7
x₃	15	\|15-16\| = 1
x₄	17	\|17-16\| = 1
x₅	33	\|33-16\| = 17
x₆	40	\|40-16\| = 24
	∑	66

Una somma delle distanze minore di 66 km non si sarebbe ottenuta con nessun altro valore.

note

Se si fosse considerato come valore centrale di riferimento la media aritmetica, la somma delle distanze da questo (degli scarti assoluti) sarebbe stata 70km.

Se l'ultima attività fosse stata alla chilometrica 100 invece che 40, la mediana sarebbe stata la stessa. In generale, se fossero state diverse tutte le altre chilometriche escluse le due centrali, la mediana non sarebbe cambiata.

La mediana, è parte di un più ampio discorso: i quantili.

È infatti il quantile di ordine $\frac{1}{2}$ (divide in due la distribuzione). Altri esempi di quantili molto utilizzati sono i quartili ed i percentili, ma vengono ora considerati tutti approfondimenti che eludono il tono squisitamente introduttivo del presente lavoro.

i quantili

Volendo conoscere come individuare i quantili, è spiegato in questa pagina di approfondimento.

sommatoria e produttoria

È bene premettere alla trattazione delle medie algebriche il significato di sommatoria e produttoria. Se lo si conoscesse già si passi pure oltre.

sommatoria

La sommatoria è una notazione sintetica della somma di un insieme di addendi.

Portando un semplice esempio, si pensi al conto della spesa che ci viene calcolato alla cassa del supermercato. Si immagini di aver acquistato cinque diversi articoli i cui rispettivi prezzi siano:

articolo	prezzo €
1	14.90
2	2.50
3	8.60
4	15.50
5	3.50
spesa:	45

Indicando con p i prezzi, per distinguerli aggiungiamo un indice progressivo in pedice così da avere p₁ che indica il primo prezzo, p₂ il secondo, sino a p₅ che indica l'ultimo prezzo:

prezzi	prezzo €
p₁	14.90
p₂	2.50
p₃	8.60
p₄	15.50
p₅	3.50
S:	45

La formula che ci viene applicata alla cassa per per calcolare la spesa S, è:

S = p₁ + p₂ + p₃ + p₄ + p₅

Indicando con i l'indice progressivo dei prezzi (1, 2, ... 5) possiamo dire che la spesa è la somma dei prezzi p_i per i che va da 1 a 5.

Quindi:

S = p₁ + p₂ + ... + p₅

indicato come sommatoria è:

che si legge "sommatoria per i che va da 1 a 5 di p con i".

Avendo acquistato gli stessi articoli, ma ciascun in quantità diverse:

articolo	prezzo €	quantità
1	14.90	4
2	2.50	5
3	8.60	4
4	15.50	1
5	3.50	8
S:	150

per calcolare la spesa bisogna sommare i prodotti dei prezzi di ciascun articolo per la rispettiva quantità:

che equivale a dire:

$S = p_{1} \cdot q_{1} + p_{2} \cdot q_{2} + . . . + p_{5} \cdot q_{5}$

Non neccessariamente però si acquistano 5 articoli, se fossero stati 7 l'indice i andrebbe da 1 a 7.

In generale, indicando con n il numero degli atricoli acquistati, la formula per la spesa è:

Che è come dire che la spesa S è data dalla somma dei prodotti di ciascun prezzo e la rispettiva quantità, dal primo (i=1) all'ultimo (i=n).

curiosità

Il simbolo usato per la sommatoria è la lettera greca sigma maiuscola Σ, sigma minuscola è σ.

produttoria

La produttoria è una notazione sintetica del prodotto di un insieme di fattori.

Per la produttoria vale quanto detto sopra per la sommatoria ma, non indica la somma di un insieme di numeri, bensì il loro prodotto.

Ad esempio:

curiosità

Il simbolo usato per la produttoria è la lettera greca Pi maiuscola Π, Pi minuscola è π (detta anche p greco).

medie algebriche

Le medie algebriche sono quelle che, considerando tutti i dati, si ottengono applicando una formula matematica, quindi si applicano quando il carattere dell'indagine sia di tipo quantitativo.

Per ciascuna media algebrica, si distinguono i casi semplice e ponderata, la prima da applicarsi a distribuzioni unitarie e l'altra a distribuzioni di frequenze. Così come la frequenza è detta anche peso, così anche le medie ponderate, vengono dette anche pesate, proprio in quanto tengono conto del peso (frequenza) che le modalità hanno nella distribuzione.

Visto però che le distribuzoini unitarie si possono leggere come distribuzioni di frequenze ove la frequenza è sempre 1, allora, la regola generale e sempre applicabile è quella della media ponderata e la variante semplice, altro non è che un suo caso particolare e semplificato perché non è utile moltiplicare per qualcosa che è sempre 1.

media aritmetica

La media aritmetica di un insieme di dati numerici è quel valore che, sostituito ai dati, lascia invariata la loro somma.

La più importante media algebrica è la media aritmetica, essendo la media maggiormente utilizzata, viene detta anche semplicemente media.

Il suo valore perde di significato quando i dati presentano valori eccezionali, è cioè tanto più indicativa quanto i dati sono tra loro omogenei (per quantificare la variabilità di un insieme di dati si vedano gli indici di variabilità)

In sostanza è il rapporto tra la somma dei valori ed il loro numero.

formula

semplice	ponderata

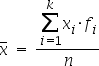esempio di media aritmetica semplice

Date 5 distanze in metri:

x_i	x
x₁	12
x₂	3
x₃	7
x₄	20
x₅	8

allora, la distanza media è:

calcolo della media aritmetica semplice

esempio di media aritmetica ponderata

Gli studenti del corso statistica descrittiva, una volta sostenuto l'esame finale, hanno ricevuto le votazioni (in punti trentesimali) rappresentate secondo la seguente distribuzione di frequenze:

x	f
16	5
18	3
22	12
25	19
27	7
30	7

allora, il voto medio è:

calcolo della media aritmetica ponderata

proprietà

Una proprietà della media aritmetica, consiste nell'essere un indice di tendenza centrale che annulla la media degli scarti da se stessa. Considerando cioè un insieme di valori di media M, i rispettivi scarti (valore - M), ovvero le distanze relative dalla media M, si compensano: la somma di quelli negativi è uguale in valore assoluto a quella degli scarti positivi, quindi la loro somma e la loro media è nulla.
Inoltre, la media aritmetica è quel valore centrale il quale, considerando il quadrato degli scarti tra ciascun dato ed essa rende minima la loro somma (quel valore centrale che rende minima la somma degli scarti è la mediana).
Per altre proprietà della media aritmetica si veda proprietà delle medie.

note

Nella formula della media aritmetica ponderata, la f utilizzata indica la frequenza assoluta, perché se si usassero le frequenze relative non occorrerebbe dividere la sommatoria per n. È infatti facilmente dimostrabile che:

dimostrazione

Si noti che se l'insieme di valori di cui si calcola la media sono tra loro uguali, la loro media sarà lo stesso valore, quindi, lo stesso ragionamento in senso opposto ci dice che se la media di un insieme di valori è K, allora, è come se essi fossero tutti uguali a K.

media quadratica

La media quadratica di un insieme di dati numerici è quel valore che, sostituito ai dati al quadrato, lascia invariata la loro somma.

È una media che trova largo utilizzo per l'analisi delle superfici ed in statistica soprattutto per la correzione degli errori ed il calcolo della dispersione (vedi deviazione standard).

In generale, si ricorre a questa media nel caso di superfici e quando la distribuzione presenta valori sia positivi sia negativi e non si vogliono considerare i segni.

In sostanza è il lato del quadrato medio: è infatti la radice quadrata del quadrato medio dei valori (intentendo con quadrato medio la media aritmetica dei valori considerati al quadrato).

formula

semplice	ponderata

esempio di media quadratica semplice

Si immagini di avere a disposizione 3 magazzini di forma quadrata per stoccare i materiali della nostra impresa, i rispettivi lati dei magazzini, misurati in metro, sono:

x_i	x
x₁	3
x₂	4
x₃	7
x₄	9
x₅	5

In questo caso, per lato medio, ci si attende quello del qudrato avente la superficie media, ovvero ci si chiede: rispetto alla superficie, qual'è il lato medio?

x	x²
3	9
4	16
7	49
9	81
5	25
Σ	180

il quadrato medio è $\frac{180}{5} = 36$ , quindi la media quadratica (il lato medio) è $\sqrt{36} = 6 m$ .

Applicando infatti la formula:

calcolo della media aritmetica ponderata

esempio di media quadratica ponderata

Misurando un stessa temperatura con 100 termometri, rispetto alla temperatura media, le misurazioni presentavano delle oscillazioni che. espresse in centesimi di grado centigrado, hanno prodotto la seguente distribuzione di frequenze::

x	f
-1.1	20
-0.1	50
0.9	30

Volendo capire la distanza media rispetto alla temperatura media rilevata, non potremo calcolare la madia artimetica, poiché otterremmo zero (vedi proproetà della media aritmetica) ne calcoleremo allora la media quadratica, così:

x	f	x²	x² · f
-1.1	20	-1.1² = 1.21	1.21·20 = 24.2
-0.1	50	-0.1² = 0.01	0.01·50 = 0.5
0.9	30	-0.9² = 0.81	0.81·30 = 24.3
Σ	100		49

Il quadrato medio è $\frac{49}{100} = 0.49$ , quindi la media quadtratica è $\sqrt{0.49} = 0.7$ centesimi di grado.

Applicando infatti la formula::

calcolo della media quadratica ponderata

Quindi, l'oscillazione standard è di 7 millesimi di grado Celsius.

proprietà

Vedi proprietà delle medie.

altre medie

Ai fini del presente corso sono strettamente necessarie soltanto la media aritmetica e la media quadratica, ma risultano a volte indispensabili anche altri indici di posizione centrale come la media geometrica e armonica.

In generale, si ricorre alla media aritmetica quando i dati di cui si vuole individuare un indice di tendenza centrale seguono una scala lineare, ma essi possono ricondursi a scale non lineari come una scala logaritmica o di reciproci nel qual caso si ricorre alle medie geometrica o armonica.

media geometrica

La media geometrica di un insieme di dati numerici è quel valore che, sostituito ai dati, lascia invariato il loro prodotto.

Sicuramente indispensabile è la media geometrica per individuare fattori di variazione medi. Serve in generale per distribuzioni che seguono una progressione geometrica: si usa quando i dati oggetto dell'indagine sono valori che per loro natura vanno tra loro moltiplicati.

In sostanza è la radice n-esima del prodotto degli n fattori.

formula

semplice	ponderata

note

La media geometrica prevede che nessuno dei valori sia nullo (perché annullerebbe il prodotto) e neanche negativo (vedi approfondimento).

esempio di media geometrica semplice

Portiamo ad esempio il caso della variazione del prezzo di un bene osservato il 1º gennaio negli anni dal al :

anno	prezzo €
	1.40
	1.75
	2.10
	2.31

Rapportando i prezzi andiamo a misurare i fattori di variazione annuali:

prezzo €	fattore di variazione	%
1.40
1.75	$F_{1} = \frac{1.75}{1.40} = 1.25$	125%
2.10	$F_{2} = \frac{2.10}{1.75} = 1.2$	120%
2.31	$F_{3} = \frac{2.31}{2.10} = 1.1$	110%

Partendo dal valore iniziale del 1.40€ e moltiplicandolo per il fattore di variazione 1.25, otterremmo il prezzo del bene misurato nel e continuando anno per anno:

$\begin{array}{l} 1 . 40€ \cdot 1.25 = 1 . 75€ \\ 1 . 75€ \cdot 1.20 = 2 . 10€ \\ 2 . 10€ \cdot 1.10 = 2 . 31€ \end{array}$

quindi:

$1 . 40€ \cdot 1.25 \cdot 1.20 \cdot 1.10 = 2 . 31€$

Indicando il valore iniziale con V_i , con F₁, F₂, ed F₃ i fattori di variazione annuali e con V_f il valore finale avremmo:

$V_{i} \cdot F_{1} \cdot F_{2} \cdot F_{3} = V_{f}$

trovando ora un fattore medio di variazione F_m si otterrebbe necessariamente che:

$V_{i} \cdot F_{m} \cdot F_{m} \cdot F_{m} = V_{f}$

ne consegue che:

$F_{1} \cdot F_{2} \cdot F_{3} = F_{m} \cdot F_{m} \cdot F_{m}$

ovvero:

$F_{1} \cdot F_{2} \cdot F_{3} = F_{m}^{3}$

che letto da destra verso sinistra ci dice:

$F_{m}^{3} = F_{1} \cdot F_{2} \cdot F_{3}$

allora:

$F_{m} = {\sqrt[3]{F_{1} \cdot F_{2} \cdot F}}_{3}$

Applicato al caso in esempio, per trovare un fattore medio di variazione operiamo la media geometrica dei tre fattori di variazione:

$\begin{array}{l} \bar{x_{g}} = \sqrt[3]{1.25 \cdot 1.20 \cdot 1.10} = \\ = \sqrt[3]{1.65} ≃ 1.1817 \end{array}$

Moltiplicando infatti il valore iniziale per la media geometrica dei fattori di variazione per tre volte otterrei il valore al terzo anno; si avrebbe ovviamente un errore usando la media aritmetica.

secondo esempio di media geometrica semplice

Conoscendo le dimensioni dei lati di un fondo agricolo di forma rettangolare, se ne ricava facilmente la superficie, si vorrebbe sapere quale lato avrebbe un fondo della stessa superficie di forma quadrata.

lato1	lato2	area	radice
25	16	$25 \cdot 16 = 400$	$\sqrt[2]{400} = 20$

Un fondo agricolo di forma quadrata e lato 20, avrebbe la stessa superficie di quello rettangolare di lati 25 e 16.

Altro non abbiamo svolto che la media geometrica dei lati, infatti, rispetto all'area, i lati sono valori che vanno tra loro moltiplicati, si cerca pertanto un valore medio il quale, se sostituito ai dati, ne lasci invariato il prodotto.

Applicando infatti la formula:

calcolo della media geometrica semplice

si ricava il lato medio.

Si noti che grazie alla media geometrica si trova il lato medio rispetto al prodotto, infatti ci interessava avere la medesima superficie, ma se avessimo voluto conoscere il lato di un fondo agricolo avente lo stesso perimetro, allora avremmo cercato un valore medio che lasciasse invariata la somma, ovvero la media aritmetica dei lati (20.5m).

esempio di media geometrica ponderata

Nella media geometrica ponderata, i fattori si ripeteranno tante volte quanto indicato come frequenza, pertanto, andandone a calcolare la media geometrica, avrei dei fattori che si ripetono, quindi una potenza.

Portiamo ad esempio quello di una una banca che propone un investimento quinquennale di 1000€ che maturano interessi con un tasso variabile:

interesse	anni
5%	3
10%	2

Nel dettaglio, gli sviluppi dell'investimento sarebbero:

anno	interesse	fattore di variazione		€
1º anno	5%	105%	1.05	1050.000
2º anno	5%	105%	1.05	1102.500
3º anno	5%	105%	1.05	1157.625
4º anno	10%	110%	1.10	1273.388
5º anno	10%	110%	1.10	1400.726

Partendo dalla nostra situazione:

x	f
1.05	3
1.10	2

calcoliamo il fattore di variazione medio:

$\begin{array}{l} \bar{x_{g}} = \sqrt[5]{1 . 05^{3} \cdot 1 . 10^{2}} = 1.0697 \end{array}$

Quindi, l'interesse medio, è:

$\begin{array}{l} 1.0697 - 1 \cdot 100 = 6.97 % \end{array}$

e non del 7% come ci direbbe erroneamente la media aritmetica.

proprietà

Vedi proprietà delle medie.

approfondimento

Perché la media geometrica non può operarsi su valori negativi?

Deriva dalla sua definizione, infatti:

$\begin{array}{l} \bar{x_{g}} = \sqrt[n]{\prod_{i = 1}^{n} x_{i}} \\ \bar{x_{g}} = \sqrt[n]{x_{1} \cdot x_{2} \cdot . . . \cdot x_{n}} \\ \log \bar{x_{g}} = \log \sqrt[n]{x_{1} \cdot x_{2} \cdot . . . \cdot x_{n}} \\ \log \bar{x_{g}} = \log (x_{1} \cdot x_{2} \cdot . . . \cdot x_{n})^{\frac{1}{n}} \\ \log \bar{x_{g}} = \frac{\log x_{1} \cdot x_{2} \cdot . . . \cdot x_{n}}{n} \\ \log \bar{x_{g}} = \frac{\log x_{1} + \log x_{2} + . . . + \log x_{n}}{n} \end{array}$

Scoprendo che il logaritmo della media geometrica è uguale alla media aritmetica dei logaritmi dei valori (la base è indifferente), si capisce perché questi non possano essere valori negativi.

media armonica

La media armonica di un insieme di dati numerici è quel valore che, sostituito ai dati, lascia invariata la somma dei loro reciproci.

È una media utile quando il fenomeno da indagare è dato dal reciproco dei dati rilevati, ovvero quando il fenomeno in oggetto segue una scala dei reciproci.

Si usa ad esempio la media armonica quando si studia la produttività (reciproco del tempo) o anche il potere di acquisto di una moneta (reciproco del prezzo).

In sostanza è il reciproco della media dei reciproci.

formula

semplice	ponderata

note

La media armonica prevede che nessino dei valori sia nullo perché lo zero non ha reciproco.

esempio di media armonica semplice

Ad esempio portiamo il caso di una casa automobilistica di autovetture che dispone di 6 linee di montaggio e vuole confrontare i tempi (in giorni) che le linee impiegano a montare la stessa autovettura.

linea	x
1	4
2	6
3	8
4	6
5	8
6	6

Si noti che la produttività è data dal reciproco del tempo ( $\frac{1}{x_{i}}$ ), misura cioè il lavoro compiuto nell'unità di tempo. Ad esempio, la produttività della linea 1, che monta l'auto in 4 giorni, è $\frac{1}{x_{i}}$ , ovvero monta $\frac{1}{4}$ di auto al giorno.

La media armonica dei tempi si calcola così:

x	1/x
4	1/4
6	1/6
8	1/8
6	1/6
8	1/8
6	1/6
Σ	24/24

la produttività media è $\frac{\frac{24}{24}}{6} = \frac{1}{6}$ quindi il tempo medio è il suo reciproco: $\frac{1}{\frac{1}{6}} = 6 g$ .

Applicando infatti la formula:

calcolo della media armonica semplice

esempio di media armonica ponderata

Se i tempi delle linee di montaggio appena visti ci fossero stati forniti sotto forma di distribuzione di frequenze:

x	f
4	1
6	3
8	2

allora avremmo dovuto calcolare la media armonica ponderata:

calcolo della media armonica ponderata

proprietà

Vedi proprietà delle medie.

proprietà delle medie

Parlando di proprietà delle medie enumeriamo le principali:

sommando o sottraendo a tutti i valori uno stesso valore K, allora la loro media sarà aumentara o diminuita di K.
moltiplicando o dividendo tutti i valori per uno stesso valore k, allora la loro media crescerà o diminuirà di K volte.

Quindi, in sinstesi, la media subisce la stessa variazione se la subiscono tutti i valori.

Nella seguente tabella è mostrato quali di queste due proprietà valgano per ciascuna delle medie trattate:

	1	2
media aritmetica	•	•
media quadratica		•
media geometrica		•
media armonica		•

Forse poi, non è inutile precisare che se l'insieme di valori è compreso tra un minimo m ed un massimo M, allora la loro media è necessariamente interna al medesimo intervallo (vero per tutte le quattro medie analizzate):

$s e \forall x_{i} \in ℝ, i = 1, . . ., n : m ⩽ x_{i} ⩽ M \Rightarrow m ⩽ \bar{x} ⩽ M$ .

media generalizzata

Probabilmente non si è notato che le quattro medie analizzate, si possono ricondurre ad una stessa generica media. Questa è detta media generalizzata o media di potenza.

In sostanza è la redice p-esima della media aritmetica dei valori elevati all'esponente p.

formula

semplice	ponderata

Si noti che a seconda del valore di p, otterremo una delle quattro medie viste.

Infatti avremo:

con p = 1, M₁ = media aritmetica.
con p = 2, M₂ = media quadratica.
con p → 0, M₀ = media geometrica.
con p =-1, M_-1= media armonica.

ordine delle medie

Nel caso i valori siano tutti uguali, allora le loro quattro medie sarebbero tutte uguali ai dati, altrimenti, i loro valori saranno crescenti al crescere di p.

$M_{- 1} ⩽ M_{0} ⩽ M_{1} ⩽ M_{2}$